Quincunx
1982. Rollie Tesh.
Pente in 8.
No captures.

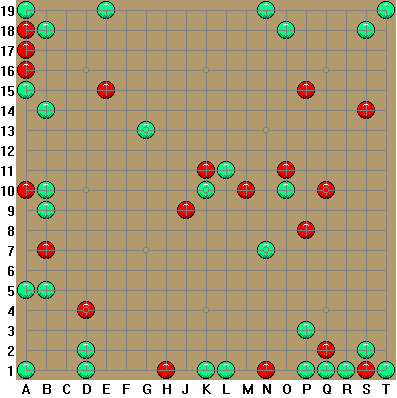
The diagram above is "Quincunx", a Pente® problem I created in early 1982. After three months of work and two months of proofreading, the problem was published in Pente® Strategy: Book II as part of a contest. A spot in the 1983 World Championship would go to the best solution sent in before December 31, 1982.

Although many entries were received, only two people correctly solved Quincunx: John Hawkins of Austin, TX, and Robert Argleden, of Colorado Springs, CO. The qualification spot went to Hawkins, whose solution was more concise and complete. (Argleden bounced back by winning the Salt Lake City Regional.)

(Hawkins surprised many prognosticators and round up in the finals of the 1983 Championship against the favored Tesh. The problem creator beat the problem solver and won the title, a trip to California, the Pente® Cup, the custom championship board and $5000. SPJ)

If you haven't yet attempted Quincunx, try to solve it yourself before reading further.

The key to understanding the solution is realizing that Quincunx is composed of two "separate" problems that are all subtly connected to a single key intersection. One of these sections runs down the left side of the board and across the bottom. The other runs from the upper left along the diagonal to the right. The solution is summarized below.

The key move, 1. L7U7!, activates both sections of the problem. The succeeding White moves are subtle double-threats, leaving Black only a choice among spectacular deaths. There are two possibilities:

A) Black blocks the "lower half" with any move on that line, such as 1. ... L5D9. White replies 2. R2U2! (His threat is then to play 3. R3U3, R4U4 4. R6U6*, R4U4 5. R7U7, R5U5 6. R7U5, R5U7* 7. R6U6*, R4U4 8.R5U5 winning in 8 moves.)

If black stops this "upper right" threat with, say, 2. ... R3U3, then White plays 3. R5D5! (and now threatens 4. R5D6, R5D8 5. R5D4, R5D3 6. R5D1*, R5D3 7. R3U1, R1U3 8. R6D2 winning). If Black blocks this threat with, say, 3. ... R5D6 then 4. L1U1! is the killer. (Now if 4. ... L2U2 White wins by 5. R2D2!, R1D1* 6. R6D6, R4D4* 7. R7D7!) So, Black plays 4. ... R1D1. Then 5. L2U2, L4U4 6. L6U6*, L4U4 7.L5U5 winning. Notice how the first move, 1. L7U7, is crucial in the final winning variation here.

If Black blocks the threats mentioned under A), with say, 1. ... R2U2*, then 2. L5D9! activates the other half of the problem. White then threatens 3. L7D9 (winning along the bottom) and 3. L8U2 (winning along the side). Black can't stop both. E.G.:

B1) 2. ... L8U2 (blocking the side) 3. L7D9 (forcing 3. ... L8D9 4. L4D9, L3D9 5. L1D9*, L3D9 6. L2D9, R2D9 7. R4D9*, R2D9 8.R3D9 winning.

B2) 2. ... L7D9 (blocking the above threat) 3. L8U2! is the killer. (Now if 3. ... L8U3 then 4. L8U1, L8D2 5. L8D4*, L8D2 6. L8D6!, L7D7 7. L8D7, L8D8 8. L8D3 winning.) So, Black tries 3. ... L8U1, but White wins by 4. L8U6!, L6U8 5. L8U5, L8U3 6. L8U7, pente. Notice again how the key move is used in the final variation. Without this stone, White could not win in time.

Rollie Tesh, "The QUINCUNX SOLUTION," Pente® Newsletter Spring 1983: 4-5.